諧波分析法在非線性電路中的應用分析
諧波分析法在非線性電路中的應用:
引言:
諧波分析法是一種廣泛應用于電路分析和設計的方法。然而,在過去的研究中,諧波分析法一直被認為只適用于線性電路。本文將探討諧波分析法在非線性電路中的可行性,并介紹一些相關的應用案例。
1. 諧波分析法簡介
諧波分析法是一種基于傅里葉級數和傅里葉變換理論的電路分析方法。它可以將任意周期信號分解為一組諧波分量,從而對信號的頻譜進行分析。諧波分析法被廣泛應用于線性電路,用于分析信號的頻譜特性、濾波器設計、系統響應等。
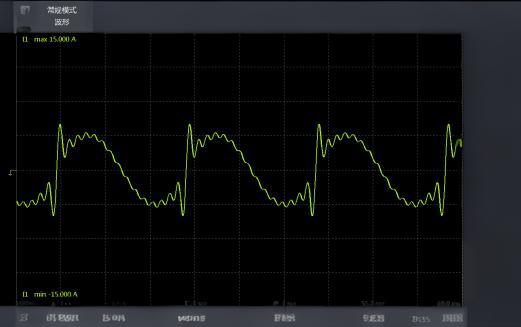
2. 非線性電路中的諧波分析問題
非線性電路在實際應用中非常常見,例如放大器、混頻器、調制器等。然而,由于非線性元件的存在,基于線性假設的諧波分析法是否適用于非線性電路一直存在爭議。非線性元件的存在會導致電路輸出信號出現諧波失真現象,這與諧波分析法的基本假設相矛盾。

3. 非線性電路中的諧波分析方法
盡管諧波分析法的基本原理是基于線性假設,但研究者們一直在努力將其應用于非線性電路。一種常見的方法是通過局部線性化,將非線性電路分解為一系列局部線性電路,并應用諧波分析法進行分析。另一種方法是采用數值模擬技術,如基于SPICE的電路仿真軟件,對非線性電路進行諧波分析。
4. 非線性電路中的諧波分析應用案例
盡管諧波分析法在非線性電路中存在一定的限制,但仍然有一些成功的應用案例。例如,在放大器設計中,通過諧波分析法可以對放大器的失真情況進行評估,從而優化電路設計。在混頻器設計中,諧波分析法可以幫助確定非線性元件的工作點,以實現更好的混頻效果。
5. 結論
在非線性電路中應用諧波分析法是一項具有挑戰性的任務。盡管諧波分析法的基本原理是基于線性假設,但通過一些創新的方法和技術,我們可以在一定程度上將其應用于非線性電路的分析和設計中。隨著技術的進步和理論的發展,相信諧波分析法在非線性電路中的應用將會取得更好的效果。
文章版權備注
- 2024-10-11能源管理系統軟件SMARTCOLLECT-PM10 ? PM20 ? PM30 二
- 2024-10-10能源管理系統軟件SMARTCOLLECT-PM10 ? PM20 ? PM30
- 2024-09-30超諧波是什么以及超諧波相關問題分析
- 2024-09-21電力監測儀是測量什么的工具
- 2024-09-21電能質量管理辦法之總則和職責
- 2024-09-21電能質量檢測儀檢測裝置是什么












 滬公網安備31011702889685
滬公網安備31011702889685
